Литература

Содержание:

Средняя школа им. Н.И. Лобачевского

Сайт: http://externlobach.ruТелефон: (8313) 34-24-23, (8313) 34-49-21Стоимость: от 2600 р. в месяц

Школа прошла все ступени государственной аккредитации и имеем официальный статус среднего общеобразовательного учреждения с правом выдачи аттестатов государственного образца при обучении учащихся со 100% использованием технологий дистанционного обучения.

Обучение с 1 по 11 класс
Государственная программа
Обучение в любом месте и в любое удобное для Вас время
Интерактивные материалы: видеолекции, тренажеры, электронные учебники и виртуальный личный кабинет для каждого ученика
Высококвалифицированные педагоги по всем предметам учебного плана
Доступная стоимость обучения
По итогам обучения Вы получаете Аттестат государственного образца

Вопросы и ответы

Вузы москвы c егэ по предмету литература (университеты, институты) — рейтинг, специальности, стоимость обучения, отзывы, проходной балл егэ 2021

Кем и когда вы были основаны?

Служение Русской Библейской Школы началось в 1991 году в Ленинграде и состояло в бесплатных рассылках Библий, Детских Библий, а также другой христианской литературы и библейских курсов, по всем регионам России. Это стало возможным благодаря усилиям нескольких христианских миссий, с некоторыми из которых мы продолжаем сотрудничать до сих пор.

На какие деньги вы существуете?

Мы существуем на пожертвования прихожан различных церквей. Кроме того, мы имеем возможность пользоваться услугами нескольких христианских издательств, которые бесплатно снабжают нас хорошими книгами.

Являетесь ли вы церковью?Нет, сами мы не являемся церковью, не организуем отдельных богослужений и не проводим таинств. Но, конечно, все наши сотрудники являются прихожанами и служителями в своих церквах.

Правда ли, что обучение и рассылки у вас бесплатные?Да, и обучение, и рассылки литературы у нас полностью бесплатны для всех наших учащихся. Единственное ограничение состоит в том, что мы не можем осуществлять бесплатные рассылки книг за пределы России.

Кто являются авторами курсов, которые вы предлагаете?Авторами наших курсов являются российские учителя и служители поместных общин, в том числе и сами сотрудники нашей библейской школы.

Каким переводом Библии вы пользуетесь?Мы стараемся пользоваться разными переводами, в том числе и оригинальным греческим текстом. Предпочтение отдаем синодальному переводу, поскольку он является наиболее распространенным среди российских верующих.

Что нужно для того, чтобы стать вашим учащимся? Для того, чтобы начать обучение, достаточно простого согласия человека. Никаких иных требований к своим учащимся мы не предъявляем. Вы можете записаться на обучение, обратившись к нам любым, наиболее удобным для вас, способом.

Как человек может спастись?Мы верим, что для спасения человек должен как минимум пройти через несколько духовных этапов, в частности: вера, покаяние, исповедь, крещение, церковь и дальнейшая жизнь в вере и благочестии. Обо всем этом мы подробно говорим на наших библейских курсах.

Необходимо ли для спасения водное крещение и почему?Да, мы верим, что водное крещение является не только желательным, но и обязательным шагом на пути спасения человека. Мы основываем свое учение по этому вопросу на отрывках из Писания (прежде всего, Деяния 2:37-38 и 1 Петра 3:21) и на опыте ранней апостольской церкви.

Каковы должны быть видимые проявления духовных даров в человеке?Мы верим, что прежде всего таким даром должна быть любовь (Иоанна 13:34-35). О других дарах мы читаем в следующих местах Нового Завета: 1 Коринф. 12:1-11, 1 Коринф. 14 глава, Галатам 5:22-23 и многих других. Духовные дары не обязательно должны иметь чудодейственную природу.

Как человек может вернуться к Богу?Если человек уже был крещен настоящим библейским крещением, но затем оставил веру, то для того, чтобы вернуться к Богу, ему необходимо глубокое раскаяние и обновление решения полностью посвятить свою жизнь Христу. Это возможно только через помощь верующих и исповедь в поместной церкви.

Как человек может возрасти в своей вере?Прежде всего, для этого необходимо твердое решение самого человека и помощь хороших духовных наставников. Заочные библейские курсы также могут быть в помощь, но они не способны полностью заменить искреннего живого общения с тем, кто глубоко знает твою жизнь, грехи, дары, сильные и слабые стороны.

Может ли верующий оставаться христианином, если не посещает церковь?Мы верим, что верующие не спасаются по одиночке. Церковь необходима для спасения, потому что предоставляет человеку возможность служить братьям и сестрам, проявлять свои духовные дары, укрепляться в веру самому и укреплять других людей, а также принимать причастие.

Русская Библейская Школа приглашает к обучению всех желающих.Мы рады служить людям и чувствуем ответственность за каждого обратившегося к нам.Если вы хотите узнать о нас больше, получить духовную литературу или начать учиться, пишите по адресу:

Эндоморфизм Фробениуса

Учитывая эллиптическую кривую , определенную над мы рассмотрим точки на более , на алгебраическое замыкание в ; т.е. мы допускаем точки с координатами в . Эндоморфизм Фробениуса из за кадром распространяется на эллиптической кривой путем .
E{\ displaystyle E}Fq{\ displaystyle \ mathbb {F} _ {q}}E{\ displaystyle E}F¯q{\ displaystyle {\ bar {\ mathbb {F}}} _ {q}}Fq{\ displaystyle \ mathbb {F} _ {q}}F¯q{\ displaystyle {\ bar {\ mathbb {F}}} _ {q}}F¯q{\ displaystyle {\ bar {\ mathbb {F}}} _ {q}}Fq{\ displaystyle \ mathbb {F} _ {q}}ϕ(Икс,y)↦(Иксq,yq){\ Displaystyle \ фи: (х, у) \ mapsto (х ^ {q}, у ^ {q})}

Эта карта является тождеством, и ее можно расширить до бесконечно удаленной точки , превратив ее в групповой морфизм из самой себя.
E(Fq){\ Displaystyle Е (\ mathbb {F} _ {q})}О{\ displaystyle O}E(Fq¯){\ displaystyle E ({\ bar {\ mathbb {F} _ {q}}})}

Эндоморфизм Фробениуса удовлетворяет квадратичному многочлену, который связан с мощностью в следующей теореме:
E(Fq){\ Displaystyle Е (\ mathbb {F} _ {q})}

Теорема: эндоморфизм Фробениуса, задаваемый формулой, удовлетворяет характеристическому уравнению
ϕ{\ displaystyle \ phi}

ϕ2-тϕ+qзнак равно,{\ Displaystyle \ phi ^ {2} -t \ phi + q = 0,} где тзнак равноq+1-#E(Fq){\ displaystyle t = q + 1 — \ # E (\ mathbb {F} _ {q})}

Таким образом, мы имеем для всего этого , где + обозначает сложение на эллиптической кривой, а и
обозначает скалярное умножение на и на .
пзнак равно(Икс,y)∈E{\ displaystyle P = (x, y) \ in E}(Иксq2,yq2)+q(Икс,y)знак равнот(Иксq,yq){\ displaystyle (x ^ {q ^ {2}}, y ^ {q ^ {2}}) + q (x, y) = t (x ^ {q}, y ^ {q})}q(Икс,y){\ Displaystyle д (х, у)}т(Иксq,yq){\ Displaystyle т (х ^ {д}, у ^ {д})}(Икс,y){\ Displaystyle (х, у)}q{\ displaystyle q}(Иксq,yq){\ displaystyle (х ^ {q}, y ^ {q})}т{\ displaystyle t}

Можно было бы попытаться символически вычислить эти точки , и как функции в из
и затем искать значение , которое удовлетворяет уравнению. Однако степени становятся очень большими, и такой подход непрактичен.
(Иксq2,yq2){\ Displaystyle (х ^ {д ^ {2}}, у ^ {д ^ {2}})}(Иксq,yq){\ displaystyle (х ^ {q}, y ^ {q})}q(Икс,y){\ Displaystyle д (х, у)} FqИкс,y(y2-Икс3-АИкс-B){\ displaystyle \ mathbb {F} _ {q} / (y ^ {2} -x ^ {3} -Ax-B)}E{\ displaystyle E}т{\ displaystyle t}

Идея Шуфа заключалась в том, чтобы выполнить это вычисление, ограничиваясь точками порядка для различных малых простых чисел . Фиксируя нечетное простое число , мы переходим к решению проблемы определения , определенного как , для данного простого числа . Если точка входит в подгруппу — кручения , то где — единственное целое число такое, что и

Обратите внимание, что и для любого целого числа у нас есть. Таким образом будет тот же порядок, что и

Таким образом, для принадлежности к , мы также имеем if . Таким образом, мы свели нашу задачу к решению уравнения
л{\ displaystyle l}л{\ displaystyle l}л{\ displaystyle l}тл{\ displaystyle t_ {l}}т(модл){\ Displaystyle т {\ pmod {l}}}л≠2,п{\ displaystyle l \ neq 2, p}(Икс,y){\ Displaystyle (х, у)}л{\ displaystyle l} Eлзнак равно{п∈E(Fq¯)∣лпзнак равноО}{\ displaystyle E = \ {P \ in E ({\ bar {\ mathbb {F} _ {q}}}) \ mid lP = O \}}qпзнак равноq¯п{\ displaystyle qP = {\ bar {q}} P}q¯{\ displaystyle {\ bar {q}}}q≡q¯(модл){\ Displaystyle д \ экв {\ бар {д}} {\ pmod {l}}}∣q¯∣

(Иксq2,yq2)+q¯(Икс,y)≡т¯(Иксq,yq),{\ displaystyle (x ^ {q ^ {2}}, y ^ {q ^ {2}}) + {\ bar {q}} (x, y) \ Equiv {\ bar {t}} (x ^ { q}, y ^ {q}),}

где и имеют целочисленные значения в .
т¯{\ displaystyle {\ bar {t}}}q¯{\ displaystyle {\ bar {q}}}-(л-1)2,(л-1)2{\ Displaystyle [- (l-1) / 2, (l-1) / 2]}

Алгоритм[править]

Описаниеправить

Алгоритм минимизации конечных автоматов Бржозовского (Janusz A. (John) Brzozowski) выделяется, по крайней мере, следующими качествами:

Он элегантен и весьма оригинален.
Он эффективен.
Он работает даже с недетерминированными конечными автоматами.

Введём следующие обозначения:

— конечный автомат,
— детерминизированный автомат для ,
— обратный автомат для ,
— результат . Аналогично для и .

Теорема (Бржозовский, 1962):

Пусть — автомат (необязательно детерминированный), распознающий язык . Минимальный детерминированный автомат может быть вычислен следующим образом: .

Доказательство:

По построению автомат детерминированный. Согласно утверждению 2, он распознает язык .
Покажем, что все правые языки различны. Из утверждения 1, левые языки попарно не пересекаются. Из утверждения 3, правые языки являются левыми языками . Таким образом, они попарно не пересекаются. Согласно утверждению 4, правый язык — объединение правых языков .
Поскольку правые языки попарно не пересекаются, все правые языки различны.

Так как все правые языки различны, согласно утверждению 5 автомат минимальный.

Пример работыправить

Исходный НКА :
Первый шаг, :
Второй шаг, :В детерминизированных автоматах состояния переименованы, так что всегда является начальным состоянием.
Третий шаг, :После выполнения этого шага алгоритма оба состояния и являются начальными.
Заключительный шаг, :

Онлайн гимназия №1

Сайт: http://онлайн-гимназия.рф Телефон: 8 (800) 100-78-54Стоимость: 15000 р. в месяц

В основе методики лежит классификация уровней познания Бенджамина Блума, американского психолога, ученого.
Суть метода: если ученик будет самостоятельно проходить первый уровень «знание» и частично второй «понимание», то дальнейшее занятие с преподавателем сможет поднять его на более высокий уровень за меньшее время в сравнении с классическим подходом

Углубленные дистанционные курсы от преподавателей ВУЗов
Участие в олимпиадах, призеры и победители которых получают дополнительные баллы к ЕГЭ при поступлении
Сертификаты участников олимпиад – дают приоритет при поступлении на платную основу
Курсы подготовки к ЕГЭ преподавателями ВУЗов
Профориентация – ранняя подготовка к специальностям в ВУЗах

Задача

Сформулируем основную задачу, которую хочется решить. Для этого сначала запишем операции над алгоритмами, которые программист выполняет в ходе написания своего проекта:

методы синтеза макро-алгоритма из под-алгоритмов (последовательной, параллельной и смешанной группировкой);
методы структурной трансформации макро-алгоритмов (оптимизационной, специализирующей, стыковочной…);
методы сохранения и переноса алгоритмов;
методы синтеза универсального алгоритма из сходных алгоритмов разных областей исполнения;
методы специализации универсального алгоритма в новой области исполнения;
методы формирования и развития комплексной системы совместно работающих алгоритмов;
методы взаимодействия одновременно исполняющихся алгоритмов;
и другие методы, полный список которых привести сложно, да и нет необходимости.

Рассмотрим существующие на текущий момент варианты значения слова «алгоритм» в поисках подсказок, о том как можно работать с алгоритмами.

Так, например, формулировка «конечная совокупность точно заданных правил решения произвольного класса задач» говорит что есть возможность как-то «точно задать правила» из них собрать «совокупность» и этой совокупностью «решить» некоторый «класс задач».

Сразу возникает масса вопросов к этому определению:

Что такое правило?
Как, кому и для кого это правило можно задать?
Что есть объединение совокупностью?
Каким образом правила соотносятся с задачей?
Что формирует класс задачи?
Определяется ли способ формирования совокупности правилами и задачами?
…

Другая формулировка «набор инструкций, описывающих порядок действий исполнителя для решения некоторой задачи» говорит что есть «исполнитель», который может выполнять некоторые «действия», и при некотором «порядке» выполнения этих «действий» «решается задача». Вопросов не стало меньше:

Какова структура набора?
Какие есть варианты действий и исполнителей?
Существуют ли минимально возможное действие, минимальный набор необходимых действий?
Каким образом действия встроены в исполнителя?
Какие есть способы создания копии исполнителя (например, если исполнитель — человек)?
Как действия зависят друг от друга в упорядоченном выполнении?
Что есть задача кроме того, что она выполняется последовательностью действий?
Как задача соотносится с исполнителем и с действиями?
Возможно ли использовать решение задачи в качестве действия?
Какие возможны варианты указания порядка действий?
Если воспроизведение патефоном записи звуков леса является алгоритмом, то какова структура этой задачи?
Если репликация ДНК является алгоритмом, то каков её исполнитель?
Если исполнителем является Машина Тьюринга, то как с её использованием решить механическую задачу, например, воспроизведение звука?

Перечислено много вопросов, но они мало помогают в поиске методов работы с алгоритмом. Поэтому поставим себе меньшую задачу, но тоже очень нам важную. Давайте попробуем сформулировать, что делает алгоритм способом решения наших задач, и какие процессы являются для него «действиями». Даже решение этой «маленькой» задачи оказывается очень объемным для одной статьи, поэтому будем его разбивать на части. И поэтому первую статью серии целиком посвятим только «Действию» и его признакам, которые опущены в указанных выше определениях алгоритма, но являются очень важными для ответов на все заданные вопросы.

Электронная гимназия АНПОО «МАНО»

Сайт: http://eschool.mano.pro/Телефон: 8 800 100 84 42, 8 (3812) 95-10-37Стоимость: от 500 рублей

Электронная гимназия АНПОО «МАНО» обучает школьников с 1 по 11 класс.

Создана с применением дистанционных образовательных технологий, порядок применения которых регламентирован Министерством просвещения РФ.

В гимназии представлены все предметы школьной программы, которые разработаны в соответствии с ФГОС. Учебные материалы (видеоуроки, конспекты, тесты, тренажёры) доступны в любое время. К каждому ученику гимназии обеспечивается индивидуальный подход.

Преимущества гимназии:

удобная организация процесса обучения,
отсутствие пространственного и временного ограничения в учебе,
доступность материала в любое время с любых электронных носителей,
возможность повторения урока неограниченное количество раз,
видео с объяснением учителя для каждого урока,
интерактивные тесты к каждому уроку,
возможность обучения в каникулы и во время карантина.

Обучаясь в гимназии, Вы сможете:

получить аттестат государственного образца;
подготовится к сдаче ВПР, ОГЭ, ЕГЭ;
подтянуть отдельные предметы, которые Вам необходимы.

Гимназия может заменить репетитора при повторении материала и поможет усвоить новые темы, если учеба дается нелегко или требует дополнительного объяснения.

В гимназию можно зачисляться для прохождения промежуточной аттестации как по всем предметам образовательной программы определенного класса, так и по отдельным предметам.

Вы можете самостоятельно выбрать удобное время и определить темп просмотра заданий, время выполнения которых не ограничено.

В создании уроков принимали участие лучшие преподаватели: кандидаты и доктора педагогических наук, высококвалифицированные специалисты, имеющие большой опыт профессиональной работы в области педагогики, психологии, менеджмента, инновационной деятельности.

В процессе обучения в гимназии учителя проверят выполненные задания, выставят оценку в электронный журнал и помогут разобрать ошибки.

Также электронная гимназия предлагает Вам авторские онлайн-курсы для детей младших и старших классов:

Школа шахмат «Mano Chess» (поступенчатый курс с нуля до уверенного шахматиста, с 6 лет);
Школа бизнеса и трейдинга «Bussines Land» (курс обучит основам ведения бизнеса-трейдинга, разработан для учеников начиная с 5 класса);
Школа «Компьютерного моделирования и программирования на языке C#» (курс обучит основам моделирования и программирования на языке C#», разработан для учеников начиная с 7 класса).

По окончание курсов вы получите официальные документы о дополнительном образовании.

Онлайн-лицей №1

Цифры: 1000 учеников, 10 лет опыта

Стоимость: 2100-25500 рублей в месяц

Куратор: есть

Подробнее: на сайте

Варианты обучения

В онлайн-лицее №1 предлагают 4 формата обучения: «Самостоятельный», «С учителями», «Зачисление», «Персональный».

«Самостоятельный» формат — это доступ к видеоурокам, электронном библиотеке, дополнительным курсам и система контроля знаний.

«С учителями» помимо программы «Самостоятельного» формата включает онлайн-консультации преподавателей, сопровождение личного куратора, подготовку к аттестациями, в том числе к ОГЭ и ЕГЭ, занятия по расписанию и проверку индивидуальных домашних заданий.

«Зачисление» — формат для тех, кто хочет полностью перейти на дистанционное обучение и получить аттестат государственного образца. В него входят программы форматов «Самостоятельный» и «С учителями».

«Персональный» формат помимо всего перечисленного предлагает ученикам индивидуальные занятия и решение нестандартных образовательных задач.

Особенности

Дистанционная подготовка к ОГЭ и ЕГЭ, личные кураторы, возможность учиться по индивидуальному графику.
Стоимость обучения в средней школе не по самостоятельной программе выше, чем у конкурентов.

Hello world

Возраст: от 7 летСайт: https://hwschool.onlineТелефон: +7(958)580−25−77Стоимость: по запросу

Если вы хотели, чтобы ваш ребенок научился программировать — в этой школе можно записать его на индивидуальные онлайн-занятия с живым преподавателем.

На первом уроке:

Ребенок напишет свою первую программу или сделает сайт;
Вы увидите, как проходят занятия, а ребенок увлечется программированием;
Ребенок увидит, что программировать гораздо интереснее, чем играть.

Предлагаемые варианты курсов:

Для начинающих

научится создавать приложения на языке Scratch;
узнает как использовать звуки, анимации и взаимодействовать с пользователем;
применит знания из школьных предметов в собственных программах;
получит постоянный доступ к учебным материалам и обновлениям;
обучение у наставника поможет расти быстрее и не забросить обучение.

Создание сайтов

возможность создавать сайты, их мобильные версии а также браузерные игры;
научится работать с программами, которые программисты используют в работе;
получит постоянный доступ к учебным материалам и обновлениям;
обучение у наставника поможет расти быстрее и не забросить обучение;
даётся возможность пройти стажировку в IT компании

Создание компьютерных программ

возможность создавать приложения и игры, запускать их у себя на компьютере и у друзей;
научится работать с программами, которые программисты используют в работе;
получит постоянный доступ к учебным материалам и обновлениям;
обучение у наставника поможет расти быстрее и не забросить обучение;
даётся возможность пройти стажировку в IT компании.

Улучшения алгоритма Шуфа

В 1990-х годах Ноам Элкис , а затем AOL Atkin , разработали улучшения базового алгоритма Шуфа, ограничив набор простых чисел, рассмотренных ранее, простыми числами определенного типа. Они стали называться простыми числами Элкиса и Аткина соответственно. Простое число называется простым числом Элкиса, если характеристическое уравнение: распадается , а простое число Аткина — это простое число, которое не является простым числом Элкиса. Аткин показал, как объединить информацию, полученную из простых чисел Аткина, с информацией, полученной из простых чисел Элкиса, для создания эффективного алгоритма, который стал известен как алгоритм Шуфа – Элкиса – Аткина . Первая проблема, которую необходимо решить, — определить, является ли данное простое число Элкисом или Аткином. Для этого мы используем модульные многочлены, которые появились в результате изучения модулярных форм и интерпретации как решеток. Как только мы определили, в каком случае мы находимся, вместо использования полиномов деления мы можем работать с полиномом, который имеет более низкую степень, чем соответствующий полином деления: а не . Для эффективной реализации используются вероятностные алгоритмы поиска корней, что делает его алгоритмом Лас-Вегаса, а не детерминированным алгоритмом. При эвристическом предположении, что примерно половина простых чисел до границы являются простыми числами Элкиса, это дает алгоритм, более эффективный, чем алгоритм Шуфа, с ожидаемым временем работы с использованием наивной арифметики и с использованием быстрой арифметики. Хотя известно, что это эвристическое предположение справедливо для большинства эллиптических кривых, известно, что оно верно не во всех случаях, даже при использовании GRH .
Sзнак равно{л1,…,лs}{\ Displaystyle S = \ {l_ {1}, \ ldots, l_ {s} \}}л{\ displaystyle l}ϕ2-тϕ+qзнак равно{\ Displaystyle \ phi ^ {2} -t \ phi + q = 0}Fл{\ displaystyle \ mathbb {F} _ {l}}О(л){\ Displaystyle О (л)}О(л2){\ Displaystyle О (л ^ {2})}О(журнал⁡q){\ Displaystyle О (\ журнал q)}О(журнал6⁡q){\ Displaystyle О (\ журнал ^ {6} q)}О~(журнал4⁡q){\ Displaystyle {\ тильда {O}} (\ log ^ {4} q)}

Университет Синергия

Сайт: https://synergy.ru/schoolСтоимость: первые 7 дней — бесплатно

Школьное онлайн-образование с 7 по 11 класс

Первая в России онлайн-школа с полноценным аккредитованным образовательным процессом
Аттестат об основном и среднем общем образовании государственного образца
Лучшие преподаватели страны
Зачисление в любое время года
Льготные условия при поступлении в ВУЗ
Полный цикл подготовки к экзаменам ОГЭ/ЕГЭ
Прохождение промежуточной аттестации онлайн
Пробные ЕГЭ и ОГЭ по вариантам от методистов ФИПИ
Отчеты успеваемости для детей и родителей

Как устроен образовательный процесс

Обучение

Проверенные и актуальные программы обучения
Общение с преподавателями в режиме реального времени
Подготовка к поступлению в лучшие вузы страны и сдаче ОГЭ
Текущая, промежуточная и итоговые аттестации

Работа на уроке

Совместная с классом работа над задачами, вопросами и материалом
Возможность в любой момент задать вопрос учителю
Интерактивная доска, сопровождающий конспект-презентация, двусторонняя аудио/видеосвязь, чат
Сохраненная запись вебинара — всегда можно вернуться и посмотреть

Поддержка

У каждого ученика есть свой куратор, к которому всегда можно обратиться за помощью через мессенджеры или позвонить
По каждому предмету оказывает поддержку наставник, которому можно задать вопросы по учебному материалу и ДЗ

Самостоятельная работа

Записи всех вебинаров, электронная библиотека и огромное количество дополнительных тестов, заданий и материалов для самостоятельной проработки
Домашние задания, состоящие из двух частей — интерактивного теста и письменной части
Результаты первой части отображаются мгновенно, а письменная часть проверяется преподавателем

Точки контроля знаний

Регулярно проводятся плановые онлайн-контрольные и экзамены по всем предметам, как и в обычной школе
К каждой теме любой дисциплины представлены дополнительные тесты и задания, которые ученик может проработать в любое время

4. Шведский стол

Столовая в «Алгоритме успеха» работает по системе шведский стол. Это значит, что ученики могут сами выбрать, что они хотят съесть сегодня: в мясной день, к примеру, им предложат сразу три блюда из мяса, приготовленные разными методами (варёное, тушёное, котлета). Три разных блюда – в рыбный день. И так каждый день.

В школе постоянно экспериментируют с меню и корректируют его с нового учебного года. Повара гордятся тем, что научили ребят есть молочные каши на завтрак и даже брокколи, к которым поначалу дети были абсолютно равнодушны.

Столовая вмещает 380 детей, поэтому едят они по расписанию: пока обедают 2–5-е классы, остальные гуляют на улице. И наоборот. 40-минутная прогулка каждый день – обязательная часть школьного дня.

Что дает обучение в школе “Алгоритм”

Обучение в нашей школе – это свобода воли каждого ученика. Есть возможность онлайн планировать расписание, контролировать домашнее задание и следить за отметками. Все это сопровождается комментариями учителей, что также можно посмотреть онлайн.

Более 100 педагогов-кураторов по отдельным предметам сопровождают учащихся на каждом этапе обучения. Все материалы, необходимые для обучения и самоподготовки, расположены на интерактивном учебном портале школы. Ребятам доступны ресурсы и все условия для дополнительного саморазвития, активного отдыха и занимательного досуга.

Мы гарантируем высокий уровень знаний, активное развитие и широкие возможности для поступления в любой российский и зарубежный ВУЗ, благодаря высоким экзаменационным результатам.

Время работы[править]

Для начала рассчитаем место, необходимое для выполнения алгоритма. Алгоритм использует рекурсивную функцию . Последовательность вызовов функции может занять память. Эта последовательность может быть представлена как путь корня рекурсивного дерева, до узла. Соответствующий вызов этого узла занимает памяти, каждый его «предок» занимает памяти, а остальные структуры используют . Очевидно, что любой путь от корня рекурсивного дерева до какого-то узла .

В итоге для работы алгоритма требуется памяти.

Лемма (#2):

Доказательство:

Утверждение напрямую вытекает из и очевидного факта, что для любого множества , количество концов отрезков, лежащих в полосе , меньше чем .

Теорема (#1):

Доказательство:

Утверждение напрямую вытекает из и следующего отношения .

Обозначим множество всех вершин рекурсивного дерева за .

Теорема (#2):

Доказательство:

Для всех узлов, кроме корня имеет место выражение , следовательно .

Начальная сортировка и инициализация множеств и может быть произведена за времени. Время работы функции является суммой длительностей всех его вызовов. Каждый вызов от внешних узлов добавляет к этой сумме . Для внутренних же узлов, время требуемое для поиска равно , а для остальных . Если мы все это сложим, то придем к выводу, что наш алгоритм работает за . Заметим, что его скорость можно увеличить до , если не будем учитывать время нахождения .

Соответственно в оптимальном алгоритме Балабана находится за .

Проблема

Текущее состояние в области программирования — это обучение ремеслу по большей части личной практикой или разборами примеров стороннего кода, с которым по каким-то причинам приходится сталкиваться.

В результате программированию учишься по наитию. Лишь немного в этом труде помогают сборники алгоритмов, прикладных техник и шаблонов проектирования. Общая совокупность предлагаемых ими рецептов выстраивается длинным списком, и его длина грозит каждому из прочитанных приемов быть позабытым (как была забыта 53-яя личная группа в «телеге» до введения разбиения по каталогам). Но даже тот прием, который остался в памяти, чаще всего просто является описанием прикладной задачи, в которой было успешно его использование.

Почему конкретный прием был успешен в задаче-образце? Будет ли он успешен в твоём проекте? Какие признаки проекта дают понять, что использование приёма уместно?

В личном опыте существования в профессии не раз отмечено, что каждый Junior борется с одинаковыми ветряными мельницами и постигает методы создания программ основываясь только на своих ошибках. Но ведь такие ошибки совершили уже очень многие. Почему до сих пор не создана система правил программирования, которая поможет обойти новоиспеченному кораблю-программисту подводные прибрежные камни? Ну, например, объяснение вреда использования метода «Copy-Paste» для развития кода. Если такие правила получится объяснить малым набором причин, их сформировавшим, то это объяснение обеспечит их запоминание и последующее использование в практике, тем самым поможет уклониться от бесчисленных грабель, разложенных тут и там.

Для компактного и полезного набора объяснений нужно:

систематизировать методы работы с кодом;
разобрать по группам приёмы работы с алгоритмами, которые являются главной целью написания любого кода;
выделить простые признаки применения шаблонов проектирования;
разработать универсальные правила и наборы эффективных способов построения сложных алгоритмов.

Если обобщить, то нужны алгоритмы для написания и развития алгоритмов.

Задуманная серия статей не претендует на полное решение указанной проблемы. Предпринимается небесспорная попытка сделать первый шаг на пути к этому решению. Этот шаг состоит в выделении структуры и свойств главного кирпичика программиста — Алгоритма.

Алгоритм за O(n3)[править]

Рассмотрим сначала наивный метод, который строит дерево за время , где — длина исходной строки . В дальнейшем данный алгоритм будет оптимизирован таким образом, что будет достигнута линейная скорость работы.

Определение:

Неявное суффиксное дерево (англ. implicit suffix tree, IST) строки — это суффиксное дерево, построенное для строки без добавления .

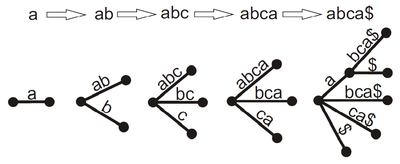
Пример построения суффиксного дерева алгоритмом Укконена.

Алгоритм последовательно строит неявные суффиксные деревья для всех префиксов исходного текста . На -ой фазе неявное суффиксное дерево для префикса достраивается до для префикса . Достраивание происходит следующим образом: для каждого суффикса подстроки необходимо спуститься от корня дерева до конца этого суффикса и дописать символ .

Алгоритм состоит из фаз. На каждой фазе происходит продление всех суффиксов текущего префикса строки, что требует времени. Следовательно, общая асимптотика алгоритма составляет .

Псевдокод алгоритма за O(n3)править

 for i = 1 .. n
   for j = 1 .. i
     treeExtend(s)

Замечание: на первый взгляд, более логичным подходом кажется добавление всех суффиксов строки в дерево по очереди, получив сразу алгоритм со временем работы . Однако осуществить улучшение данного алгоритма до линейного времени работы будет намного сложней, хотя именно в этом и заключается суть алгоритма МакКрейта.

Разбираем «на пальцах»

Вот Алексей. Он обычный парень, который любит играть в футбол. Нам необходимо прописать программу, симулирующую игру Лёши. Для этого мы прописываем конкретную инструкцию, которая состоит из таких команд:

Надеть спортивную одежду.
Взять мяч.
Выйти на улицу.
Поставить мяч на землю.
Ударить по мячу.

Запускаем игру и понимаем, что что-то идёт не так. Причина в том, что Алексей вышел играть в туфлях, а не в спортивной обуви, так как мы не учли в инструкции этот нюанс.

Возвращаемся назад и дополняем:

Надеть спортивную одежду.
Надеть спортивную обувь.
Взять мяч.
Выйти на улицу.
Поставить мяч на землю.
Ударить по мячу.

Теперь игра идёт так, как мы задумали.

Этот вариант примитивный. В настоящей программе инструкций будет гораздо больше. Каждое действие Алексея придётся прописывать подробно. Например, выход из дома:

Открыть дверь.
Выйти.
Закрыть дверь.
Подойти к лифту.
Нажать на кнопку.
Зайти в лифт.
Нажать кнопку первого этажа.
Выйти из лифта и т. д.

Чем подробнее прописаны стейтменты, тем более качественно работает программа.

Представьте количество команд, инструкций и сложность алгоритма в искусственном интеллекте или роботе. Сколько подробных инструкций предусматривает и прописывает программист, чтобы искусственный интеллект самостоятельно принимал решения, а робот ходил, разговаривал, отвечал и реагировал на действия.

В случае с Алексеем, дополнительно понадобилось бы прописать и то, что он идёт на выбранную спортивную площадку или стадион, зовёт с собой друзей и т. д.

Учитывайте тот факт, что ваша программа обязательно будет изменяться и дополняться. Тот, кто после вас займётся её поддержкой и развитием, должен понять вашу логику. Не слишком стремитесь к упрощению и минималистичности.